algorithmic modeling for Rhino
Hi there,
I drew an oloid by using the functions:
 ;
;  ;
;  and
and
 ;
; 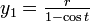 ;
; 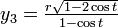 ;
;
If I use any equal spaced range of t(x) on ![t \in \left[\tfrac{\pi}{3},\tfrac{5\pi}{3}\right]](http://upload.wikimedia.org/math/c/e/c/cec704cf91ede0c65ea58a86cef23791.png) ; I will end up with an unequal range t(y), which looks like this:
; I will end up with an unequal range t(y), which looks like this:
My goal is to have an symmetric spacing by remaping t(x).
I tried to use the GraphMapper with a parabolic distribution for t(x) and it almost right but still off.
(I am using half the domain to make sure I have a curve on the axis.)
How do I remap t(x) to get the right result?
Asking for help, please.
Thanks,
Phillip
Views: 3154
- Attachments:
Replies to This Discussion
-
Just quickly threw this together, without diving into the functions. I only had time to quickly replicate the geometry and divide those.
If you simple make two circles, shatter those to get the subdomain you need [1/3pi; 5/3pi] and then divide those into equal segments, you get two arcs with equally spaced points. Then shift list one of the list of points [wrap=TRUE], make lines between these points and you're done. Be sure to use an even number of devisions and the amount of shift is then ([LengthList]+1)/2. This is to make sure that the endpoint of one arc connects to the middle of the other arc.
I understand it's the quick and dirty version just to get the points, so if it's the mapping you're after you need to do the math.
- Attachments:
-
-
Thanks for the reply. Though it is not really what I am looking for.
I am searching for a mathematical solution to speed things up. So I am looking for an equation that describes the relation between the points given by the equations mentioned above and a way to implement it.
Nevertheless, unfortunatly it also doesn´t solve the problem. If you just connect the equal spaced points this is what you get:
At least two of the main properties of the geometry: 1; All lines will be have the same length and 2; The View from front will follow a square like this:
wont be fullfilled like this.
This means the distribution can´t be a linear.
Really banging my head on this one...
-
-
Since you already inked to wikipedia, did you read the PDF by Hellmuth Stachel and Hans Dirnböck?
I just had a quick glance at it but I guess the answer to your question of how to map the t param should be in there, or at least pointers to it.
-
-
Hi Hannes, as you would have guessed, I already went trough this paper before. But since I wasn´t sure what exact term or definition I am looking for (Winkelgeschwindigkeit?) it ended in a pathetic random trial and error. Maybe you can just point me to it? Thanks.
-
-
Hey Philip,
I was affraid that was too easy :). So now for math version...
Since the speed on each arc differs, I made two separate parameters. t for the lying arc, s for the one standing upright. The next step was to define the points on the two curves in terms of t and s. Point A for the lying arc and point B for the one standing.
A=r*{-cos(t), -sin(t),0} 0<t<2/3*pi
B=r*{1-cos(s),0,sin(s)} pi/3<s<pi
When t=0, s=pi/3 [that's the line from the middle of the lying arc to the end of the one standing upright]
This can be used to calculate the distance between the two points. Some basic geometry gives that
|AB|=r*sqrt(3)
This can be used to get an expression for s in terms of t. That means that we can express the position of point B in terms of t.
Let's first find the function s(t). Distance in 3 dimensions is given by sqrt((x1-x2)^2+(y1-y2)^2+(z1-z2)^2). When we apply this to the coordinates of A and B we get
|AB|=r*sqrt{(1-cos(s)+cos(t))^2+(sin(t))^2+(sin(s))^2}
The part in the root has to be equal to 3 [see |AB| above]. When we get rid of all the brackets we get:
3-2cos(s)+2cos(t)-2cos(s)cos(t)=3 [we used: cos^2(t)+sin^2(t)=1]
so cos(s)=cos(t)/(1+cos(t))
or: s=arccos(cos(t)/(1+cos(t))
Now you can get the mapping from A to B, both depending on parameter t.
Hopefully this is what you were looking for :D
By the way, this is only for one quarter of the shape, but the rest is trivial due to symmetry.
-
- Attachments:
-
-
Thank you so much for your efforts Reinier.
At first glance at your text, I thought we got now. Unfortunatly as your picture reveals, its still not solving the problem. The distribution of points on the cosrresponding curves is still not point-symmetric.
To illustrate, I merged our definitons and it shows (with yours being the more elegant obviously) they are more or less the same.
The question is not so much how to get the corresponding points, but how to distribute t(x)?
- Attachments:
-
-
If I am seeing it right, I think the issue is that there actually can't be a construction of an oloid comprised of lines drawn between points evenly spaced on the two circles, regardless of the domain supplied in t(x).
The points described for X {r*cos(t),0,r*sin(t)} will be evenly spaced only when your domain between Pi/3 and 5*Pi/3 is evenly divided; therefore any deviation from this state will automatically prevent an even distribution on one of your constructing circles...so you can make your Y points more evenly distributed, but only at the expense of the even distribution for all X points.
Am I misunderstanding your purpose?
-
-
Yes, a little. I am not looking for an even distribution, but for an point symmetric one.
So if my Arcs are A and B, then the length segments for A should be the same as the reversed for B.
The answer would be a (probably quite easy) function that lets me remap the input t before drawing the oloid lines.
I made a little illustration. I think the pink dots show the graph of the function i am looking for.
As you see the parabolic distribution i used is almost right.
- Attachments:
-
-
If you achieve this, your oloid will no longer be an oloid; the asymmetrical nature of the X and Y point locations is essential to the oloid's construction...or maybe not...I see what you're getting at...
-
-
so there may be some trigonometric function to achieve the management of t you're looking for dynamically, but perhaps an easier way to solve it is to change how you're constructing your points. Basically the inflection point that's most important for you is at Pi/2, which is where the line gets drawn around which you want your symmetry to occur. So if you set your range to run from Pi/3 to Pi/2, you actually get pretty much all of the information you need to construct your lists of points. With a little reversing, addition/subtraction and shifting of x/y/z inputs, you can replicate symmetrical points throughout.
- Attachments:
-
-
Hi David,
true, the lines are symmetric without any doubt.
Unfortunatly it still doesn´t give me, what I have been looking for, which can probably only be solved by the trogonometric function. I guess my discribtion has been to vague. I think I am looking for the dependency of the divisions to achieve a harmonic division.
Meanwhile I tried to use the graph of function from Reinier - s=arccos(cos(t)/(1+cos(t) - to remap which came close again, but still was wrong.
Hope I will find the (probably embarrassing simple) answer soon.
To be continued...
Still thanks a lot!
Best,
Phillip
-
© 2026 Created by Scott Davidson.
Powered by
![]()