Carrying on from the post on Classical Geometries in architecture, this post collects some of the contemporary computational geometries in architecture:

CONTEMPORARY AND PARAMETRIC GEOMETRIES IN ARCHITECTURE

Carrying on from the previous list of historical geometries in architecture, it’s time to look into contemporary geometry typologies. These increasingly depend on mathematics and scientific theories like Systems Thinking, but the list below does not go into these in detail but will give you a broad overview of some of the concepts.

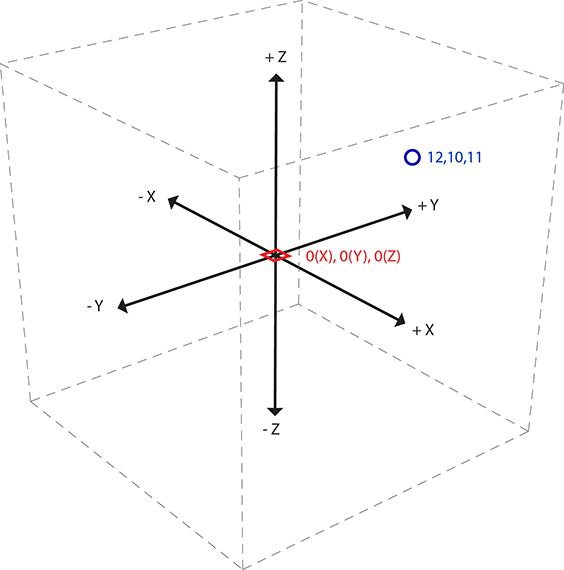
CARTESIAN COORDINATION SYSTEM

The 17^th century also saw the invention of a method to describe forms in a 2 or 3-dimensional space using numerical coordinates. Starting at an origin point, (in 3D) three mutually perpendicular axis (x, y and z) form a three-dimensional numerical grid. The combination of topology, vectors, and the co-ordinates are the basis of any Computer Aided Design space.

CALCULUS TO TOPOLOGY

In the 17^th century Calculus, the mathematical study of continuous change, leads to new evaluation of forms and form calculation.

Topology is distinct from geometry within mathematics. Topology engages in the properties of geometric objects with continuous deformations, such as pulling, pushing, twisting, stretching, crumpling and bending, but not assembling, stacking, cutting or adhering like classical geometries.

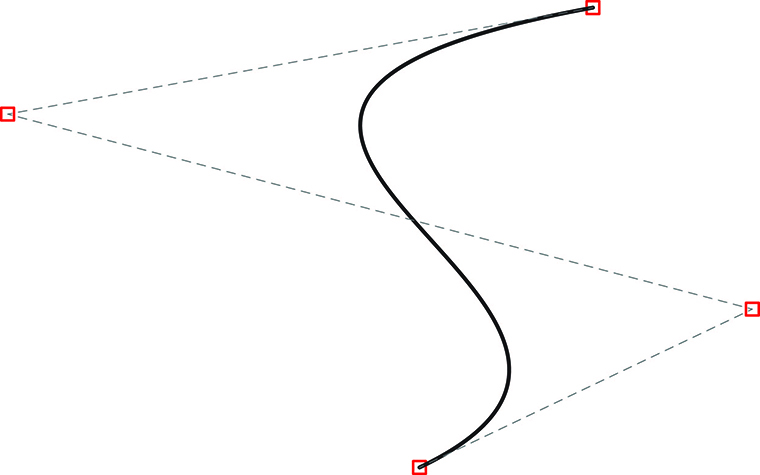
SPLINE

Originally a long thin strip of wood used by boat builders to draw smooth shapes. A spline is at its core a polynomial line controlled by variable points. The curve does not have a uniformly straight or circular segments as each segment between control points will be affected by points beyond the immediate control points. For this reason, splines and spline-based surfaces are considered by many as the fundamental parametric design language.

SINGLE SURFACE

The Möbius strip has been mentioned before as a classical geometry. This is a simple ruled geometry where a strip of 2D surface is joined into a continual rotated surface. A surface that is effectively one sided. Klein bottle is the 3-Dimensional version of the same mathematical concept. The idea of single surfaces has been prevalent in parametric design approaches with attempts at breaking down clear distinctions between building elements (wall, floor, ceiling etc.)

Further reading at https://www.thorarchitects.com/parametric-geometry/